Detailed guide to setting priors
James Uanhoro
priors.RmdDefault priors
We begin by loading the package:
## ## ################################################################################# This is minorbsem 0.2.15##
## All users of R (or SEM) are invited to report bugs, submit functions or ideas
## for functions. An efficient way to do this is to open an issue on GitHub
## https://github.com/jamesuanhoro/minorbsem/issues/.## ###############################################################################The default priors are:
priors_default <- new_mbsempriors()
priors_default## An object of class "mbsempriors"
## Slot "lkj_shape":
## [1] 2
##
## Slot "ml_par":
## [1] 0
##
## Slot "sl_par":
## [1] 1
##
## Slot "rs_par":
## [1] 1
##
## Slot "rc_par":
## [1] 2
##
## Slot "sc_par":
## [1] 0.5
##
## Slot "rm_par":
## [1] 0.15
lkj_shape
The lkj_shape parameter is for setting priors on the
interfactor correlation matrix. By default this value is 2, and implies
each correlation in the matrix follows the distribution: \(\frac{r + 1}{2} \sim \text{Beta}(a, a)\),
where \(a = \eta + \frac{d - 2}{2}\),
where \(\eta\) is the
lkj_shape parameter and \(d\) is the number of factors. For example,
for three factors and \(\eta = 5\),
\(a = 5 + (3 - 2) / 2 = 5.5\), so each
correlation follows the distribution: Beta(5.5, 5.5). Assuming \(\eta = 20\), we have Beta(20.5, 20.5). Both
distributions are visualized below.
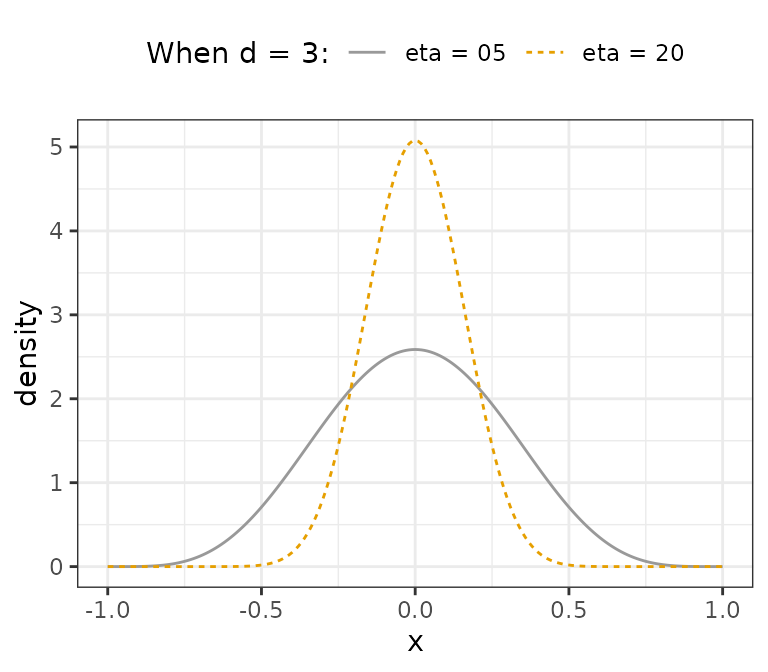
We see that larger values of lkj_shape can be used to
constrain interfactor correlations.
ml_par and sl_par
ml_par and sl_par are the prior mean and SD
for loadings which are assumed to be normally distributed. Note that
factors are assumed to be standardized.
rs_par
Residual standard deviation parameters are assumed to follow a
location-scale Student-t distribution with degrees of freedom 3
(unchangeable), location 0 (unchangeable) and scale
rs_par.
rc_par
Residual correlations between indicators assumed \(\text{Beta}(a, a)\) where \(a = \mathsf{rc\_par}\).
sc_par
All coefficients in minorbsem are assumed to be
standardized. These coefficients are assumed normal with mean 0
(changeable, see section on latent
regression below) and SD of sc_par.
Simple changes to default priors
Holzinger-Swineford example
This dataset is discussed in the CFA tutorial.
## x1 x2 x3 x4 x5 x6 x7 x8 x9
## 1 3.333333 7.75 0.375 2.333333 5.75 1.2857143 3.391304 5.75 6.361111
## 2 5.333333 5.25 2.125 1.666667 3.00 1.2857143 3.782609 6.25 7.916667
## 3 4.500000 5.25 1.875 1.000000 1.75 0.4285714 3.260870 3.90 4.416667
## 4 5.333333 7.75 3.000 2.666667 4.50 2.4285714 3.000000 5.30 4.861111
## 5 4.833333 4.75 0.875 2.666667 4.00 2.5714286 3.695652 6.30 5.916667
## 6 5.333333 5.00 2.250 1.000000 3.00 0.8571429 4.347826 6.65 7.500000The scale of data is important for setting priors on model
parameters. The default priors for models fit with
minorbsem are reasonable when variables have standard
deviations close to 1. For this reason, we first check the standard
deviations of the relevant variables for this analysis:
apply(item_data, 2, sd) # compute SD of each variable## x1 x2 x3 x4 x5 x6 x7 x8 x9
## 1.167432 1.177451 1.130979 1.164116 1.290472 1.095603 1.089534 1.012615 1.009152All variables have standard deviations close to 1, so we can move forward with the data as they are. Otherwise, we would recommend re-scaling the variables.1
syntax_basic <- "
Visual =~ x1 + x2 + x3
Verbal =~ x4 + x5 + x6
Speed =~ x7 + x8 + x9"Let’s fit the model with modified priors:
priors_modified <- new_mbsempriors(lkj_shape = 10, sl_par = .75)
priors_modified## An object of class "mbsempriors"
## Slot "lkj_shape":
## [1] 10
##
## Slot "ml_par":
## [1] 0
##
## Slot "sl_par":
## [1] 0.75
##
## Slot "rs_par":
## [1] 1
##
## Slot "rc_par":
## [1] 2
##
## Slot "sc_par":
## [1] 0.5
##
## Slot "rm_par":
## [1] 0.15We can fit make the call to the minorbsem() function and
obtain the data list passed to Stan instead of fitting the model by
setting ret_data_list = TRUE:
base_dl <- minorbsem(
syntax_basic, item_data,
priors = priors_modified, ret_data_list = TRUE
)## Processing user input ...
base_dl$shape_phi_c # reflects the shape of interfactor correlation matrix## [1] 10
base_dl$load_est # reflects prior mean for loadings## Visual Verbal Speed
## x1 0 0 0
## x2 0 0 0
## x3 0 0 0
## x4 0 0 0
## x5 0 0 0
## x6 0 0 0
## x7 0 0 0
## x8 0 0 0
## x9 0 0 0
base_dl$load_se # reflects prior SD for loadings## Visual Verbal Speed
## x1 0.75 0.75 0.75
## x2 0.75 0.75 0.75
## x3 0.75 0.75 0.75
## x4 0.75 0.75 0.75
## x5 0.75 0.75 0.75
## x6 0.75 0.75 0.75
## x7 0.75 0.75 0.75
## x8 0.75 0.75 0.75
## x9 0.75 0.75 0.75
base_dl$loading_pattern # shows indices for non-zero loadings## Visual Verbal Speed
## x1 1 0 0
## x2 2 0 0
## x3 3 0 0
## x4 0 4 0
## x5 0 5 0
## x6 0 6 0
## x7 0 0 7
## x8 0 0 8
## x9 0 0 9We can either run the model with:
base_mod <- minorbsem(syntax_basic, item_data, priors = priors_modified)or
base_mod <- minorbsem(data_list = base_dl, priors = priors_modified)The results would be identical. Adding
priors = priors_modified is optional.2
Examples of priors on specific loadings and coefficients
Small variance prior on all cross-loadings
Following Muthén and Asparouhov (2012),
one can estimate all cross-loadings by placing small variance priors on
them. Note that minorbsem contains a cleaner approach to the same task
with models of the form:
minorbsem(..., simple_struc = FALSE). But we demonstrate
the small variance approach to show how to set specific priors on some
loadings.
syntax_cross <- paste(
paste0("Visual =~ ", paste0("x", 1:9, collapse = " + ")),
paste0("Verbal =~ ", paste0("x", 1:9, collapse = " + ")),
paste0("Speed =~ ", paste0("x", 1:9, collapse = " + ")),
sep = "\n"
)
writeLines(syntax_cross)## Visual =~ x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9
## Verbal =~ x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9
## Speed =~ x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9Then we call minorbsem() with
ret_data_list = TRUE to obtain the data list:
small_var_dl <- minorbsem(syntax_cross, item_data, ret_data_list = TRUE)## Processing user input ...Set all cross-loadings to have prior SDs of 0.1:
small_var_dl$load_se## Visual Verbal Speed
## x1 1 1 1
## x2 1 1 1
## x3 1 1 1
## x4 1 1 1
## x5 1 1 1
## x6 1 1 1
## x7 1 1 1
## x8 1 1 1
## x9 1 1 1
small_var_dl$load_se[4:9, 1] <- 0.1
small_var_dl$load_se[-c(4:6), 2] <- 0.1
small_var_dl$load_se[1:6, 3] <- 0.1
small_var_dl$load_se## Visual Verbal Speed
## x1 1.0 0.1 0.1
## x2 1.0 0.1 0.1
## x3 1.0 0.1 0.1
## x4 0.1 1.0 0.1
## x5 0.1 1.0 0.1
## x6 0.1 1.0 0.1
## x7 0.1 0.1 1.0
## x8 0.1 0.1 1.0
## x9 0.1 0.1 1.0Before fitting the model, minorbsem automatically identifies an indicator per factor that it uses to align the factor in the right direction. Given that all indicators reflect all factors, we would need to identify these indicators manually:
small_var_dl$markers## [1] 1 1 1
small_var_dl$markers <- c(1, 4, 7) # for visual, verbal and speed respectivelyThen fit the model:
small_var_mod <- minorbsem(data_list = small_var_dl)## Parameter estimates (method = normal, sample size(s) = 301)
## from op to mean sd 5.000% 95.000% rhat ess_bulk
## ───────────────────────────────────────────────────────────────────────────────
## Goodness of fit
## ───────────────────────────────────────────────────────────────────────────────
## PPP 0.447 1.000 1670
## RMSE 0.027 0.013 0.006 0.051 1.003 495
## ───────────────────────────────────────────────────────────────────────────────
## Factor loadings
## ───────────────────────────────────────────────────────────────────────────────
## Visual =~ x1 0.758 0.118 0.574 0.957 1.001 1426
## Visual =~ x2 0.560 0.105 0.379 0.732 1.002 2339
## Visual =~ x3 0.749 0.111 0.572 0.937 1.003 1533
## Visual =~ x4 0.036 0.074 -0.087 0.155 1.000 2632
## Visual =~ x5 -0.063 0.079 -0.194 0.065 1.000 2446
## Visual =~ x6 0.070 0.071 -0.048 0.184 1.000 2507
## Visual =~ x7 -0.142 0.079 -0.271 -0.012 1.002 2580
## Visual =~ x8 0.004 0.081 -0.128 0.132 1.000 2369
## Visual =~ x9 0.209 0.076 0.078 0.325 1.002 2125
## Verbal =~ x1 0.122 0.080 -0.012 0.248 1.001 2216
## Verbal =~ x2 0.014 0.073 -0.108 0.133 1.001 3225
## Verbal =~ x3 -0.078 0.075 -0.205 0.041 1.000 2805
## Verbal =~ x4 0.979 0.080 0.853 1.113 1.003 2356
## Verbal =~ x5 1.139 0.087 0.992 1.285 1.003 1834
## Verbal =~ x6 0.885 0.072 0.770 1.006 1.001 2249
## Verbal =~ x7 0.022 0.073 -0.099 0.143 1.000 2201
## Verbal =~ x8 -0.039 0.076 -0.163 0.083 1.001 2270
## Verbal =~ x9 0.032 0.068 -0.079 0.141 1.002 2410
## Speed =~ x1 0.054 0.080 -0.082 0.182 1.000 2580
## Speed =~ x2 -0.051 0.077 -0.175 0.076 1.000 2941
## Speed =~ x3 0.041 0.079 -0.088 0.169 1.002 2355
## Speed =~ x4 0.002 0.072 -0.113 0.121 1.000 2904
## Speed =~ x5 0.006 0.078 -0.121 0.132 1.000 2747
## Speed =~ x6 0.002 0.068 -0.110 0.115 1.001 2679
## Speed =~ x7 0.732 0.100 0.568 0.903 1.004 1394
## Speed =~ x8 0.779 0.098 0.625 0.951 1.007 1432
## Speed =~ x9 0.542 0.089 0.401 0.694 1.001 1891
## ───────────────────────────────────────────────────────────────────────────────
## Inter-factor correlations
## ───────────────────────────────────────────────────────────────────────────────
## Verbal ~~ Visual 0.353 0.110 0.165 0.522 1.001 1781
## Speed ~~ Visual 0.330 0.128 0.113 0.530 1.002 1795
## Speed ~~ Verbal 0.245 0.117 0.047 0.431 1.000 2009
## ───────────────────────────────────────────────────────────────────────────────
## Residual variances
## ───────────────────────────────────────────────────────────────────────────────
## x1 ~~ x1 0.663 0.141 0.416 0.869 1.000 1678
## x2 ~~ x2 1.085 0.114 0.904 1.278 1.000 2318
## x3 ~~ x3 0.732 0.133 0.514 0.942 1.000 1475
## x4 ~~ x4 0.375 0.090 0.220 0.514 1.005 1526
## x5 ~~ x5 0.421 0.116 0.239 0.612 1.005 1340
## x6 ~~ x6 0.373 0.073 0.251 0.486 1.001 2206
## x7 ~~ x7 0.702 0.120 0.503 0.897 1.005 1369
## x8 ~~ x8 0.447 0.120 0.229 0.626 1.007 1288
## x9 ~~ x9 0.584 0.081 0.452 0.712 1.001 2522
## ───────────────────────────────────────────────────────────────────────────────
##
##
## Column names: from, op, to, mean, sd, 5%, 95%, rhat, ess_bulkPriors on specific coefficients
Consider the latent regression model:
syntax_reg <- "
Visual =~ x1 + x2 + x3 + x9
Verbal =~ x4 + x5 + x6
Speed =~ x7 + x8 + x9
Verbal ~ Visual + Speed"Assume we believe the most likely estimate of the coefficient from visual to verbal is .5, we can change the prior mean for this coefficient to .5. We first retrieve the data list object.
reg_dl <- minorbsem(
syntax_reg, item_data,
ret_data_list = TRUE
)## Processing user input ...
reg_dl$coef_pattern # coefficient pattern, note non-zero cells## Visual Verbal Speed
## Visual 0 0 0
## Verbal 1 0 2
## Speed 0 0 0
reg_dl$coef_est # default prior means## Visual Verbal Speed
## Visual 0 0 0
## Verbal 0 0 0
## Speed 0 0 0
reg_dl$coef_est["Verbal", "Visual"] <- .5
reg_dl$coef_est # updated## Visual Verbal Speed
## Visual 0.0 0 0
## Verbal 0.5 0 0
## Speed 0.0 0 0
reg_dl$coef_se # default prior SDs## Visual Verbal Speed
## Visual 0.5 0.5 0.5
## Verbal 0.5 0.5 0.5
## Speed 0.5 0.5 0.5Then we fit the model with the updated data list:
reg_mod <- minorbsem(data_list = reg_dl)## Parameter estimates (method = normal, sample size(s) = 301)
## from op to mean sd 5.000% 95.000% rhat ess_bulk
## ──────────────────────────────────────────────────────────────────────────────
## Goodness of fit
## ──────────────────────────────────────────────────────────────────────────────
## PPP 0.385 1.001 1668
## RMSE 0.037 0.012 0.017 0.058 1.007 493
## ──────────────────────────────────────────────────────────────────────────────
## Latent regression coefficients (outcome ~
## predictor)
## ──────────────────────────────────────────────────────────────────────────────
## Verbal ~ Visual 0.419 0.075 0.292 0.538 1.017 970
## Verbal ~ Speed 0.080 0.078 -0.049 0.203 1.001 2382
## ──────────────────────────────────────────────────────────────────────────────
## R square
## ──────────────────────────────────────────────────────────────────────────────
## Visual ~~ Visual 0.000 0.000 0.000 0.000
## Verbal ~~ Verbal 0.209 0.059 0.117 0.310 1.014 1741
## Speed ~~ Speed 0.000 0.000 0.000 0.000
## ──────────────────────────────────────────────────────────────────────────────
## Factor loadings
## ──────────────────────────────────────────────────────────────────────────────
## Visual =~ x1 0.912 0.100 0.752 1.081 1.001 1318
## Visual =~ x2 0.501 0.088 0.361 0.645 1.000 2756
## Visual =~ x3 0.650 0.088 0.504 0.797 1.001 2462
## Visual =~ x9 0.400 0.079 0.270 0.531 1.002 1921
## Verbal =~ x4 0.994 0.073 0.875 1.114 1.000 1626
## Verbal =~ x5 1.080 0.077 0.957 1.210 1.000 2259
## Verbal =~ x6 0.931 0.072 0.818 1.053 1.003 1018
## Speed =~ x9 0.439 0.088 0.296 0.584 1.005 1184
## Speed =~ x7 0.649 0.097 0.497 0.812 1.004 1242
## Speed =~ x8 0.848 0.109 0.672 1.026 1.004 853
## ──────────────────────────────────────────────────────────────────────────────
## Inter-factor correlations
## ──────────────────────────────────────────────────────────────────────────────
## Verbal ~~ Visual 0.000 0.000 0.000 0.000
## Speed ~~ Visual 0.271 0.088 0.129 0.411 1.000 2315
## Speed ~~ Verbal 0.000 0.000 0.000 0.000
## ──────────────────────────────────────────────────────────────────────────────
## Residual variances
## ──────────────────────────────────────────────────────────────────────────────
## x1 ~~ x1 0.534 0.157 0.257 0.774 1.003 1117
## x2 ~~ x2 1.141 0.110 0.970 1.329 1.000 2908
## x3 ~~ x3 0.859 0.106 0.687 1.040 1.001 2054
## x9 ~~ x9 0.582 0.082 0.451 0.716 1.000 1890
## x4 ~~ x4 0.365 0.101 0.195 0.529 1.002 1126
## x5 ~~ x5 0.500 0.116 0.313 0.688 1.003 1499
## x6 ~~ x6 0.341 0.097 0.172 0.480 1.004 643
## x7 ~~ x7 0.772 0.118 0.572 0.955 1.005 1172
## x8 ~~ x8 0.316 0.166 0.017 0.567 1.006 554
## ──────────────────────────────────────────────────────────────────────────────
##
##
## Column names: from, op, to, mean, sd, 5%, 95%, rhat, ess_bulkWe also show results from the fit with default priors:
reg_def_priors <- minorbsem(syntax_reg, item_data)## Parameter estimates (method = normal, sample size(s) = 301)
## from op to mean sd 5.000% 95.000% rhat ess_bulk
## ──────────────────────────────────────────────────────────────────────────────
## Goodness of fit
## ──────────────────────────────────────────────────────────────────────────────
## PPP 0.379 1.003 1558
## RMSE 0.037 0.013 0.018 0.059 1.005 622
## ──────────────────────────────────────────────────────────────────────────────
## Latent regression coefficients (outcome ~
## predictor)
## ──────────────────────────────────────────────────────────────────────────────
## Verbal ~ Visual 0.418 0.074 0.293 0.537 1.004 2558
## Verbal ~ Speed 0.078 0.078 -0.050 0.208 1.002 2386
## ──────────────────────────────────────────────────────────────────────────────
## R square
## ──────────────────────────────────────────────────────────────────────────────
## Visual ~~ Visual 0.000 0.000 0.000 0.000
## Verbal ~~ Verbal 0.208 0.058 0.116 0.305 1.002 3137
## Speed ~~ Speed 0.000 0.000 0.000 0.000
## ──────────────────────────────────────────────────────────────────────────────
## Factor loadings
## ──────────────────────────────────────────────────────────────────────────────
## Visual =~ x1 0.904 0.098 0.750 1.078 1.000 2170
## Visual =~ x2 0.496 0.090 0.350 0.647 1.001 2823
## Visual =~ x3 0.647 0.084 0.511 0.786 1.001 2360
## Visual =~ x9 0.398 0.080 0.264 0.526 1.001 2522
## Verbal =~ x4 0.993 0.074 0.874 1.115 1.002 2105
## Verbal =~ x5 1.084 0.081 0.955 1.223 1.000 2673
## Verbal =~ x6 0.926 0.068 0.820 1.040 1.002 2108
## Speed =~ x9 0.442 0.085 0.304 0.583 1.000 1896
## Speed =~ x7 0.650 0.099 0.495 0.812 1.004 1608
## Speed =~ x8 0.844 0.106 0.669 1.022 1.002 1293
## ──────────────────────────────────────────────────────────────────────────────
## Inter-factor correlations
## ──────────────────────────────────────────────────────────────────────────────
## Verbal ~~ Visual 0.000 0.000 0.000 0.000
## Speed ~~ Visual 0.270 0.087 0.123 0.410 1.001 2714
## Speed ~~ Verbal 0.000 0.000 0.000 0.000
## ──────────────────────────────────────────────────────────────────────────────
## Residual variances
## ──────────────────────────────────────────────────────────────────────────────
## x1 ~~ x1 0.545 0.155 0.268 0.785 1.001 1811
## x2 ~~ x2 1.144 0.113 0.966 1.337 1.000 3362
## x3 ~~ x3 0.861 0.106 0.692 1.039 1.000 2422
## x9 ~~ x9 0.578 0.082 0.448 0.715 1.000 1963
## x4 ~~ x4 0.365 0.102 0.200 0.523 1.000 1712
## x5 ~~ x5 0.489 0.122 0.292 0.690 1.002 1740
## x6 ~~ x6 0.346 0.090 0.190 0.486 1.002 1483
## x7 ~~ x7 0.771 0.122 0.573 0.960 1.005 1492
## x8 ~~ x8 0.323 0.161 0.025 0.574 1.002 1214
## ──────────────────────────────────────────────────────────────────────────────
##
##
## Column names: from, op, to, mean, sd, 5%, 95%, rhat, ess_bulkWorks Cited
Muthén, Bengt, and Tihomir Asparouhov. 2012. “Bayesian Structural
Equation Modeling: A More Flexible Representation of
Substantive Theory.” Psychological Methods 17 (3):
313–35. https://doi.org/10.1037/a0026802.