Confirmatory Factor Analysis
Xiaolu Fan, James Uanhoro
cfa.RmdBasic CFA Model
We begin with a simple example of confirmatory factor analysis (CFA),
using theminorbsem() function to fit the model. The
minorbsem package contains a built-in dataset called
HS, which is a part of classic Holzinger-Swineford dataset.
This dataset is used in many papers and books on CFA. The dataset
consists of mental ability test scores of seventh and eighth grade
children from two different schools (Pasteur and Grant-White). In our
version of the dataset (obtained from lavaan, Rosseel (2012)), only 9 out of the original 26
tests are included.
We begin by loading the package:
## ## ################################################################################# This is minorbsem 0.2.15##
## All users of R (or SEM) are invited to report bugs, submit functions or ideas
## for functions. An efficient way to do this is to open an issue on GitHub
## https://github.com/jamesuanhoro/minorbsem/issues/.## ###############################################################################The first six lines of the dataset:
head(HS)## id sex ageyr agemo school grade x1 x2 x3 x4 x5 x6 x7 x8
## 1 1 1 13 1 Pasteur 7 3.333333 7.75 0.375 2.333333 5.75 1.2857143 3.391304 5.75
## 2 2 2 13 7 Pasteur 7 5.333333 5.25 2.125 1.666667 3.00 1.2857143 3.782609 6.25
## 3 3 2 13 1 Pasteur 7 4.500000 5.25 1.875 1.000000 1.75 0.4285714 3.260870 3.90
## 4 4 1 13 2 Pasteur 7 5.333333 7.75 3.000 2.666667 4.50 2.4285714 3.000000 5.30
## 5 5 2 12 2 Pasteur 7 4.833333 4.75 0.875 2.666667 4.00 2.5714286 3.695652 6.30
## 6 6 2 14 1 Pasteur 7 5.333333 5.00 2.250 1.000000 3.00 0.8571429 4.347826 6.65
## x9
## 1 6.361111
## 2 7.916667
## 3 4.416667
## 4 4.861111
## 5 5.916667
## 6 7.500000Data preparation
The scale of data is important for setting priors on model
parameters. The default priors for models fit with
minorbsem are reasonable when variables have standard
deviations close to 1. For this reason, we first check the standard
deviations of the relevant variables for this analysis:
## x1 x2 x3 x4 x5 x6 x7 x8 x9
## 1 3.333333 7.75 0.375 2.333333 5.75 1.2857143 3.391304 5.75 6.361111
## 2 5.333333 5.25 2.125 1.666667 3.00 1.2857143 3.782609 6.25 7.916667
## 3 4.500000 5.25 1.875 1.000000 1.75 0.4285714 3.260870 3.90 4.416667
## 4 5.333333 7.75 3.000 2.666667 4.50 2.4285714 3.000000 5.30 4.861111
## 5 4.833333 4.75 0.875 2.666667 4.00 2.5714286 3.695652 6.30 5.916667
## 6 5.333333 5.00 2.250 1.000000 3.00 0.8571429 4.347826 6.65 7.500000
apply(item_data, 2, sd) # compute SD of each variable## x1 x2 x3 x4 x5 x6 x7 x8 x9
## 1.167432 1.177451 1.130979 1.164116 1.290472 1.095603 1.089534 1.012615 1.009152All variables have standard deviations close to 1, so we can move forward with the data as they are. Otherwise, we would recommend re-scaling the variables.1
Model syntax
The model syntax is lavaan-style:
syntax_basic <- "
Visual =~ x1 + x2 + x3
Verbal =~ x4 + x5 + x6
Speed =~ x7 + x8 + x9"This model assumes three latent variables (or factors): visual, verbal, and speed. The visual factor has the indicators: x1, x2, and x3; the verbal factor has indicators: x4, x5, and x6; the speed factor has indicators: x7, x8, and x9.
Fit the model
We run the analysis using the minorbsem() function. By
default, the function assumes that minor factors influence the
covariance between the variables. minorbsem then prints out
the iterations from Stan – we show these iterations once so the reader
knows what to expect.
fit_cfa <- minorbsem(model = syntax_basic, data = HS)## Processing user input ...## User input fully processed :)
## Now to modeling.## Fitting Stan model ...## Init values were only set for a subset of parameters.
## Missing init values for the following parameters:
## - chain 1: gdp_alpha, loadings, res_sds_u, phi_mat_chol, res_cor_01, coefs, sigma_loadings_complex, gdp_loadings_complex, Sigma
## - chain 2: gdp_alpha, loadings, res_sds_u, phi_mat_chol, res_cor_01, coefs, sigma_loadings_complex, gdp_loadings_complex, Sigma
## - chain 3: gdp_alpha, loadings, res_sds_u, phi_mat_chol, res_cor_01, coefs, sigma_loadings_complex, gdp_loadings_complex, Sigma
##
## To disable this message use options(cmdstanr_warn_inits = FALSE).## Running MCMC with 3 chains, at most 2 in parallel...
##
## Chain 1 Iteration: 1 / 2000 [ 0%] (Warmup)## Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:## Chain 1 Exception: lkj_corr_cholesky_lpdf: Random variable[2] is 0, but must be positive! (in '/tmp/RtmpjepldW/model-20773924bfe6.stan', line 324, column 2 to column 48)## Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,## Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.## Chain 1## Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:## Chain 1 Exception: lkj_corr_cholesky_lpdf: Random variable[2] is 0, but must be positive! (in '/tmp/RtmpjepldW/model-20773924bfe6.stan', line 324, column 2 to column 48)## Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,## Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.## Chain 1## Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:## Chain 1 Exception: cholesky_decompose: A is not symmetric. A[1,4] = inf, but A[4,1] = inf (in '/tmp/RtmpjepldW/model-20773924bfe6.stan', line 432, column 6 to column 81)## Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,## Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.## Chain 1## Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:## Chain 1 Exception: cholesky_decompose: Matrix m is not positive definite (in '/tmp/RtmpjepldW/model-20773924bfe6.stan', line 432, column 6 to column 81)## Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,## Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.## Chain 1## Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:## Chain 1 Exception: lkj_corr_cholesky_lpdf: Random variable[2] is 0, but must be positive! (in '/tmp/RtmpjepldW/model-20773924bfe6.stan', line 324, column 2 to column 48)## Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,## Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.## Chain 1## Chain 1 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:## Chain 1 Exception: lkj_corr_cholesky_lpdf: Random variable[2] is 0, but must be positive! (in '/tmp/RtmpjepldW/model-20773924bfe6.stan', line 324, column 2 to column 48)## Chain 1 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,## Chain 1 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.## Chain 1## Chain 2 Iteration: 1 / 2000 [ 0%] (Warmup)## Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:## Chain 2 Exception: cholesky_decompose: A is not symmetric. A[1,2] = inf, but A[2,1] = inf (in '/tmp/RtmpjepldW/model-20773924bfe6.stan', line 432, column 6 to column 81)## Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,## Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.## Chain 2## Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:## Chain 2 Exception: cholesky_decompose: A is not symmetric. A[1,2] = inf, but A[2,1] = inf (in '/tmp/RtmpjepldW/model-20773924bfe6.stan', line 432, column 6 to column 81)## Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,## Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.## Chain 2## Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:## Chain 2 Exception: cholesky_decompose: Matrix m is not positive definite (in '/tmp/RtmpjepldW/model-20773924bfe6.stan', line 432, column 6 to column 81)## Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,## Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.## Chain 2## Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:## Chain 2 Exception: cholesky_decompose: Matrix m is not positive definite (in '/tmp/RtmpjepldW/model-20773924bfe6.stan', line 432, column 6 to column 81)## Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,## Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.## Chain 2## Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:## Chain 2 Exception: lkj_corr_cholesky_lpdf: Random variable[2] is 0, but must be positive! (in '/tmp/RtmpjepldW/model-20773924bfe6.stan', line 324, column 2 to column 48)## Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,## Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.## Chain 2## Chain 2 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:## Chain 2 Exception: cholesky_decompose: A is not symmetric. A[7,8] = inf, but A[8,7] = inf (in '/tmp/RtmpjepldW/model-20773924bfe6.stan', line 432, column 6 to column 81)## Chain 2 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,## Chain 2 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.## Chain 2## Chain 1 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 2 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 1 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 2 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 2 Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 1 Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 2 Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 1 Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 2 Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 2 Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 2 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 1 Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 1 Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 2 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 2 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 1 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 2 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 1 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 2 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 2 finished in 3.2 seconds.
## Chain 3 Iteration: 1 / 2000 [ 0%] (Warmup)## Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:## Chain 3 Exception: lkj_corr_cholesky_lpdf: Random variable[2] is 0, but must be positive! (in '/tmp/RtmpjepldW/model-20773924bfe6.stan', line 324, column 2 to column 48)## Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,## Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.## Chain 3## Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:## Chain 3 Exception: lkj_corr_cholesky_lpdf: Random variable[2] is 0, but must be positive! (in '/tmp/RtmpjepldW/model-20773924bfe6.stan', line 324, column 2 to column 48)## Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,## Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.## Chain 3## Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:## Chain 3 Exception: cholesky_decompose: Matrix m is not positive definite (in '/tmp/RtmpjepldW/model-20773924bfe6.stan', line 432, column 6 to column 81)## Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,## Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.## Chain 3## Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:## Chain 3 Exception: cholesky_decompose: Matrix m is not positive definite (in '/tmp/RtmpjepldW/model-20773924bfe6.stan', line 432, column 6 to column 81)## Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,## Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.## Chain 3## Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:## Chain 3 Exception: lkj_corr_cholesky_lpdf: Random variable[2] is 0, but must be positive! (in '/tmp/RtmpjepldW/model-20773924bfe6.stan', line 324, column 2 to column 48)## Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,## Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.## Chain 3## Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:## Chain 3 Exception: cholesky_decompose: Matrix m is not positive definite (in '/tmp/RtmpjepldW/model-20773924bfe6.stan', line 432, column 6 to column 81)## Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,## Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.## Chain 3## Chain 1 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 3 Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 1 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 3 Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 1 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 1 finished in 4.4 seconds.
## Chain 3 Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 3 Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 3 Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 3 Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 3 Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 3 Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 3 Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 3 Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 3 Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 3 finished in 4.0 seconds.
##
## All 3 chains finished successfully.
## Mean chain execution time: 3.9 seconds.
## Total execution time: 7.4 seconds.
##
## Parameter estimates (method = normal, sample size(s) = 301)
## from op to mean sd 5.000% 95.000% rhat ess_bulk
## ──────────────────────────────────────────────────────────────────────────────
## Goodness of fit
## ──────────────────────────────────────────────────────────────────────────────
## PPP 0.415 1.002 1796
## RMSE 0.064 0.015 0.042 0.090 1.005 750
## ──────────────────────────────────────────────────────────────────────────────
## Factor loadings
## ──────────────────────────────────────────────────────────────────────────────
## Visual =~ x1 0.939 0.127 0.733 1.153 1.003 1024
## Visual =~ x2 0.470 0.105 0.303 0.644 1.001 1708
## Visual =~ x3 0.624 0.105 0.452 0.795 1.001 1868
## Verbal =~ x4 1.000 0.094 0.848 1.158 1.002 1092
## Verbal =~ x5 1.064 0.101 0.900 1.233 1.002 1892
## Verbal =~ x6 0.932 0.088 0.791 1.080 1.003 1034
## Speed =~ x7 0.561 0.104 0.392 0.731 1.004 1776
## Speed =~ x8 0.677 0.108 0.504 0.861 1.001 1535
## Speed =~ x9 0.785 0.118 0.595 0.999 1.002 877
## ──────────────────────────────────────────────────────────────────────────────
## Inter-factor correlations
## ──────────────────────────────────────────────────────────────────────────────
## Verbal ~~ Visual 0.424 0.079 0.293 0.552 1.001 2253
## Speed ~~ Visual 0.468 0.098 0.310 0.625 1.002 1650
## Speed ~~ Verbal 0.277 0.078 0.147 0.403 1.001 3310
## ──────────────────────────────────────────────────────────────────────────────
## Residual variances
## ──────────────────────────────────────────────────────────────────────────────
## x1 ~~ x1 0.465 0.219 0.043 0.796 1.003 920
## x2 ~~ x2 1.157 0.125 0.959 1.365 1.001 2395
## x3 ~~ x3 0.883 0.131 0.666 1.092 1.002 1634
## x4 ~~ x4 0.347 0.157 0.056 0.596 1.001 846
## x5 ~~ x5 0.520 0.178 0.209 0.806 1.002 1592
## x6 ~~ x6 0.328 0.137 0.069 0.539 1.003 786
## x7 ~~ x7 0.871 0.119 0.680 1.065 1.000 1775
## x8 ~~ x8 0.575 0.134 0.343 0.779 1.002 1506
## x9 ~~ x9 0.407 0.171 0.074 0.660 1.003 772
## ──────────────────────────────────────────────────────────────────────────────
##
##
## Column names: from, op, to, mean, sd, 5%, 95%, rhat, ess_bulkOutput structure
At the top of the results table, method = normal
indicates the approach of estimating the residual covariances between
all items: the belief is that the standardized residual covariances
(SRCs) which reflect minor factor influences are normally distributed
with zero mean. The table also prints out the sample size of 301 – only
complete rows are retained for analysis.
We describe the column headers. The from,
op and to combination describe the type of
parameter being reported according to lavaan-style syntax. For example,
the Visual =~ x1 row describes the loading from the visual
factor to item x1. The mean, sd and percentage
columns are descriptive statistics of posterior distributions. The
mean and sd function like the estimate and
standard error in standard frequentist statistics. The percentage
columns are credible intervals. By default, they are 90% credible
intervals, i.e. given the prior and data, there is a 90% chance the
parameter falls in this interval. rhat (pronounced R-hat)
and ess_bulk columns are the potential scale reduction
factor (\(\widehat{R}\)) and effective
sample size (ESS) respectively (Vehtari et al.
2021) – they are useful for checking parameter convergence. For
\(\widehat{R}\), values very close to 1
are preferable. For ESS, larger values are preferable.
A final analysis in a manuscript would ideally have all parameters with
\(\widehat{R}\) under 1.01 and ESS
above 400 for one to be sure parameter estimates have converged (Vehtari et al. 2021). An easy way to meet these
expectations is to increase the number of requested samples when calling
minorbsem() via the warmup = and
sampling = arguments, see ?minorbsem.
The parameter estimates are presented by the type of parameter.
Goodness of fit
PPP. The first section of results contains
parameters that help assess global model fit. “PPP” is the posterior
predictive p-value in the form described by Muthén and Asparouhov (2012), and is akin to a
\(\chi^2\) test in standard SEMs. It is
conventional to prefer values under .05 or .10. Here, PPP = .382
indicating a good-fitting model. Desirable PPP-values are to be expected
by default in minorbsem as the package accounts for model
misspecification – alternatively stated: PPP-values above .05 do not
imply an absence of misfit and is not all that informative by default.
We report PPP since minorbsem is also able to fit Bayesian
SEMs that do not account for misspecification,
e.g. minorbsem(..., method = "none").
RMSE. This the root mean square error of standardized residual covariances (SRCs) and communicates the typical size of SRCs. One may also interpret this metric as the standard deviation of SRCs with 95% of SRCs lying within 2 RMSE values from 0. In this example, RMSE = 0.063 and we can expect some SRCs to be greater than 0.10, suggesting some large SRCs (Maydeu-Olivares 2017). Large SRCs challenge the notion that model misspecification is due to the influence of minor factors – if these influences are large, are these factors “minor”? It is possible that the hypothesized structure is incorrect, or minor factors have significant effects.
Substantive parameters
The parameter estimates are reported by type of parameter: factor loadings, inter-factor correlations, and error variances. For this model, all items load on their respective factors with intervals that clearly exclude 0. All factors are assumed standardized in minorbsem, so only their correlations are reported; and all factors are non-trivially correlated.
Residual plots
Given that the RMSE suggests large standardized residual covariances (SRCs), we can request a plot of SRCs using two options: a range-plot and a heat-map.
plot_residuals(fit_cfa, type = "range")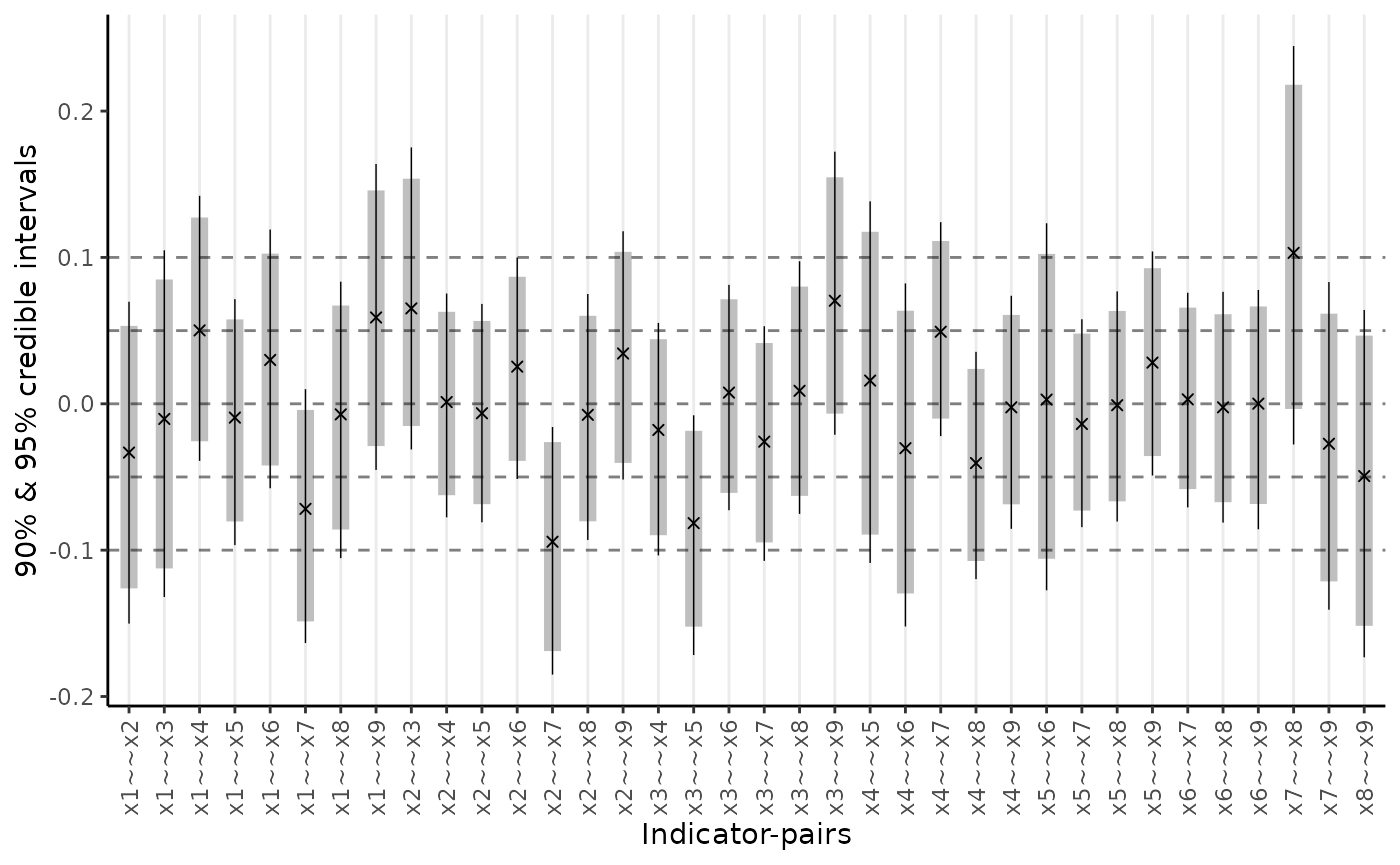
plot_residuals(fit_cfa, type = "matrix")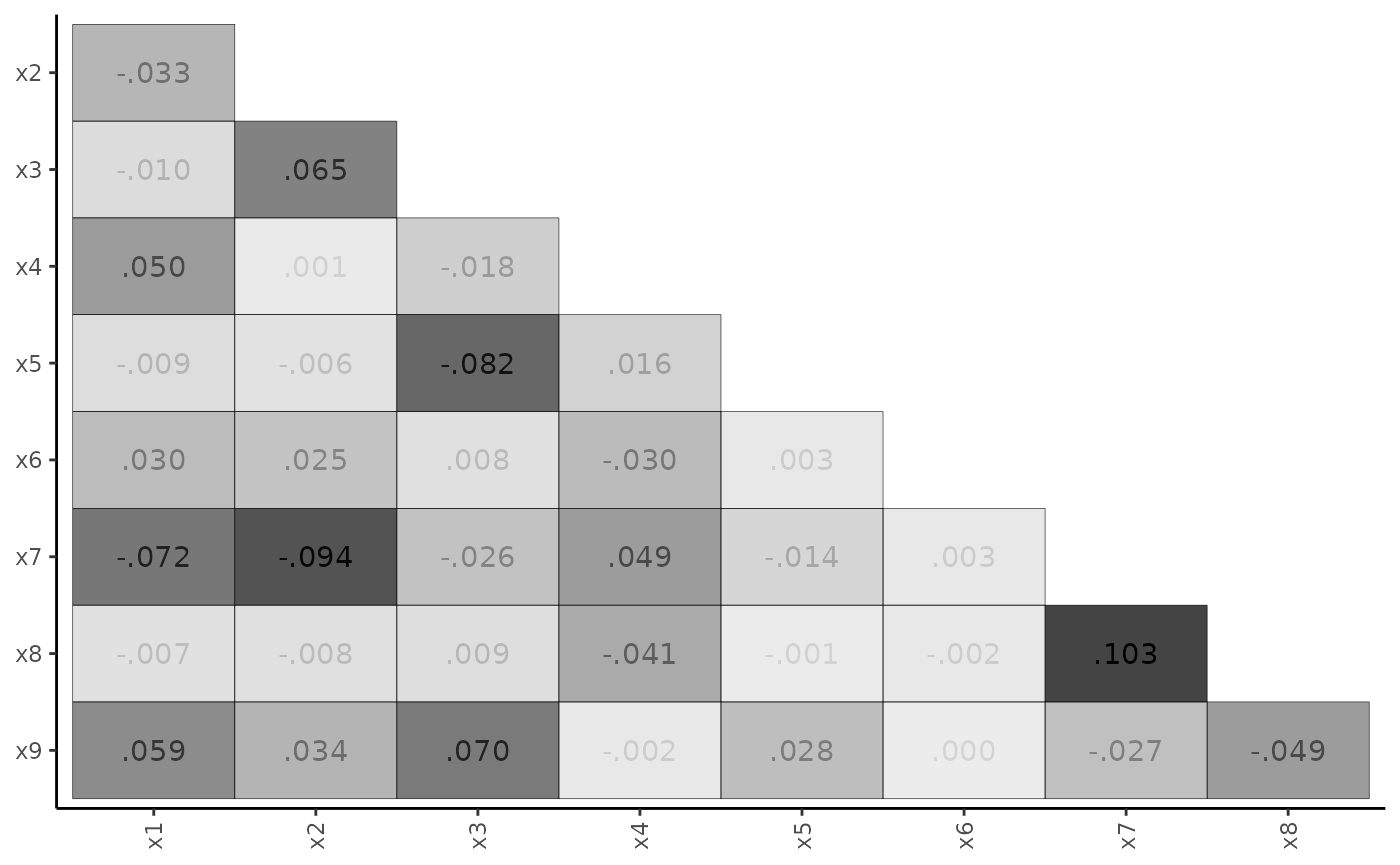
The heat-map is particularly useful for highlighting the largest SRCs. If these SRCs cluster in a non-random way, one may identify potential model modifications.
Bifactor model with orthogonal factors
To improve on the basic model, we consider the bifactor structure, which builds on the basic CFA model by specifying a general factor ‘G’ that is reflected in all nine indicators. All factors are assumed orthogonal.
Model syntax
syntax_bifactor <- paste0(
"G =~ x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9", "\n",
syntax_basic
)
writeLines(syntax_bifactor)## G =~ x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9
##
## Visual =~ x1 + x2 + x3
## Verbal =~ x4 + x5 + x6
## Speed =~ x7 + x8 + x9Fit the model
The call to minorbsem() needs to be of the form:
minorbsem(..., orthogonal = TRUE) to ensure the factors are
orthogonal:
fit_bifactor <- minorbsem(syntax_bifactor, data = HS, orthogonal = TRUE)## Parameter estimates (method = normal, sample size(s) = 301)
## from op to mean sd 5.000% 95.000% rhat ess_bulk
## ───────────────────────────────────────────────────────────────────────────────
## Goodness of fit
## ───────────────────────────────────────────────────────────────────────────────
## PPP 0.389 1.002 1484
## RMSE 0.028 0.013 0.008 0.052 1.019 464
## ───────────────────────────────────────────────────────────────────────────────
## Factor loadings
## ───────────────────────────────────────────────────────────────────────────────
## G =~ x1 0.944 0.110 0.761 1.124 1.000 1630
## G =~ x2 0.487 0.109 0.313 0.667 1.001 2056
## G =~ x3 0.623 0.100 0.451 0.787 1.000 2230
## G =~ x4 0.473 0.091 0.329 0.627 1.001 1880
## G =~ x5 0.427 0.099 0.273 0.595 1.002 2155
## G =~ x6 0.463 0.084 0.330 0.601 1.001 2237
## G =~ x7 0.109 0.088 -0.029 0.258 1.001 2357
## G =~ x8 0.287 0.078 0.165 0.417 1.000 2633
## G =~ x9 0.510 0.080 0.384 0.644 1.004 2057
## Visual =~ x1 0.223 0.178 0.015 0.591 1.000 1284
## Visual =~ x2 -0.126 0.518 -0.977 0.799 1.002 1252
## Visual =~ x3 0.013 0.473 -0.732 0.896 1.005 1451
## Verbal =~ x4 0.860 0.076 0.735 0.981 1.001 1426
## Verbal =~ x5 1.047 0.090 0.897 1.192 1.001 1627
## Verbal =~ x6 0.785 0.072 0.669 0.905 1.001 1922
## Speed =~ x7 0.725 0.118 0.538 0.925 1.000 942
## Speed =~ x8 0.714 0.113 0.534 0.924 1.002 975
## Speed =~ x9 0.431 0.082 0.293 0.561 1.001 1930
## ───────────────────────────────────────────────────────────────────────────────
## Inter-factor correlations
## ───────────────────────────────────────────────────────────────────────────────
## Visual ~~ G 0.000 0.000 0.000 0.000
## Verbal ~~ G 0.000 0.000 0.000 0.000
## Verbal ~~ Visual 0.000 0.000 0.000 0.000
## Speed ~~ G 0.000 0.000 0.000 0.000
## Speed ~~ Visual 0.000 0.000 0.000 0.000
## Speed ~~ Verbal 0.000 0.000 0.000 0.000
## ───────────────────────────────────────────────────────────────────────────────
## Residual variances
## ───────────────────────────────────────────────────────────────────────────────
## x1 ~~ x1 0.408 0.216 0.019 0.732 1.000 905
## x2 ~~ x2 0.879 0.344 0.093 1.272 1.003 731
## x3 ~~ x3 0.685 0.270 0.082 1.003 1.003 879
## x4 ~~ x4 0.388 0.093 0.237 0.535 1.002 975
## x5 ~~ x5 0.391 0.132 0.154 0.596 1.001 1117
## x6 ~~ x6 0.376 0.075 0.254 0.499 1.000 2049
## x7 ~~ x7 0.648 0.161 0.365 0.893 1.001 889
## x8 ~~ x8 0.439 0.147 0.148 0.640 1.006 960
## x9 ~~ x9 0.579 0.077 0.453 0.701 1.001 2638
## ───────────────────────────────────────────────────────────────────────────────
##
##
## Column names: from, op, to, mean, sd, 5%, 95%, rhat, ess_bulkCompared to the basic CFA model, the RMSE drops from .063 to .028, suggesting a much better fitting model. All items load with 90% intervals excluding 0 on the general factor, except for x7. Additionally, x1 – x3 load confusingly on their specific factor, while x4 – x9 load strongly on their specific factors especially when compared to their general factor loadings. This pattern of factor loadings provide little support for a bifactor structure.
Bifactor model with parameter constraints
We instead explore a more constrained bifactor structure where specific factor loadings are forced equal within each specific factor. Note that minorbsem uses the same parameter constraint syntax as lavaan:
Model syntax
syntax_bifactor_cons <- paste0(
"G =~ x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9", "\n",
"Visual =~ a * x1 + a * x2 + a * x3
Verbal =~ b * x4 + b * x5 + b * x6
Speed =~ c * x7 + c * x8 + c * x9"
)Fit the model
fit_bifactor_cons <- fit_bifactor_cons <- minorbsem(
syntax_bifactor_cons,
data = HS, orthogonal = TRUE
)## Parameter estimates (method = normal, sample size(s) = 301)
## from op to mean sd 5.000% 95.000% rhat ess_bulk
## ──────────────────────────────────────────────────────────────────────────────
## Goodness of fit
## ──────────────────────────────────────────────────────────────────────────────
## PPP 0.427 1.000 1987
## RMSE 0.048 0.012 0.030 0.071 1.003 772
## ──────────────────────────────────────────────────────────────────────────────
## Factor loadings
## ──────────────────────────────────────────────────────────────────────────────
## G =~ x1 0.867 0.116 0.669 1.056 1.003 1831
## G =~ x2 0.432 0.115 0.241 0.613 1.002 2537
## G =~ x3 0.572 0.113 0.383 0.756 1.002 1708
## G =~ x4 0.497 0.098 0.339 0.662 1.000 2116
## G =~ x5 0.489 0.113 0.308 0.684 1.000 1927
## G =~ x6 0.472 0.091 0.332 0.629 0.999 2131
## G =~ x7 0.133 0.095 -0.019 0.293 1.002 2530
## G =~ x8 0.287 0.086 0.149 0.428 1.001 2642
## G =~ x9 0.520 0.085 0.377 0.660 1.000 2555
## Visual =~ x1 0.280 0.149 0.032 0.511 1.002 1985
## Visual =~ x2 0.280 0.149 0.032 0.511 1.002 1985
## Visual =~ x3 0.280 0.149 0.032 0.511 1.002 1985
## Verbal =~ x4 0.864 0.060 0.765 0.962 1.002 1825
## Verbal =~ x5 0.864 0.060 0.765 0.962 1.002 1825
## Verbal =~ x6 0.864 0.060 0.765 0.962 1.002 1825
## Speed =~ x7 0.604 0.054 0.515 0.693 1.001 2586
## Speed =~ x8 0.604 0.054 0.515 0.693 1.001 2586
## Speed =~ x9 0.604 0.054 0.515 0.693 1.001 2586
## ──────────────────────────────────────────────────────────────────────────────
## Inter-factor correlations
## ──────────────────────────────────────────────────────────────────────────────
## Visual ~~ G 0.000 0.000 0.000 0.000
## Verbal ~~ G 0.000 0.000 0.000 0.000
## Verbal ~~ Visual 0.000 0.000 0.000 0.000
## Speed ~~ G 0.000 0.000 0.000 0.000
## Speed ~~ Visual 0.000 0.000 0.000 0.000
## Speed ~~ Verbal 0.000 0.000 0.000 0.000
## ──────────────────────────────────────────────────────────────────────────────
## Residual variances
## ──────────────────────────────────────────────────────────────────────────────
## x1 ~~ x1 0.525 0.160 0.237 0.771 1.001 1511
## x2 ~~ x2 1.106 0.120 0.917 1.307 1.000 3682
## x3 ~~ x3 0.849 0.110 0.673 1.033 1.002 2568
## x4 ~~ x4 0.352 0.081 0.216 0.485 1.000 2302
## x5 ~~ x5 0.623 0.092 0.477 0.775 1.001 2435
## x6 ~~ x6 0.250 0.082 0.108 0.382 1.004 1395
## x7 ~~ x7 0.777 0.086 0.644 0.925 1.000 4108
## x8 ~~ x8 0.568 0.072 0.452 0.691 1.001 3538
## x9 ~~ x9 0.423 0.091 0.269 0.567 1.000 2419
## ──────────────────────────────────────────────────────────────────────────────
##
##
## Column names: from, op, to, mean, sd, 5%, 95%, rhat, ess_bulkThe RMSE increased since the model is more constrained. The pattern of results with the parameter constraints imposed suggest the general factor mostly reflects items x1 – x3, with other items more strongly reflecting their specific factors. These results suggest limited applicability of the bifactor model for these data.
Non-Simple Structure Model
For our final model, we return to the original basic CFA and relax simple structure. Unlike Muthén and Asparouhov (2012) who do this using small-variance priors, minorbsem does this using a global-local prior (Uanhoro 2024). Precisely, this approach assumes that most cross-loadings are indeed zero and there are some outlier non-zero cross loadings.
Fit the model
The call to minorbsem() needs to be of the form:
minorbsem(..., simple_struc = FALSE)
fit_non_simple <- minorbsem(syntax_basic, data = HS, simple_struc = FALSE)## Parameter estimates (method = normal, sample size(s) = 301)
## from op to mean sd 5.000% 95.000% rhat ess_bulk
## ───────────────────────────────────────────────────────────────────────────────
## Goodness of fit
## ───────────────────────────────────────────────────────────────────────────────
## PPP 0.470 1.003 1786
## RMSE 0.025 0.012 0.006 0.047 1.004 513
## ───────────────────────────────────────────────────────────────────────────────
## Factor loadings
## ───────────────────────────────────────────────────────────────────────────────
## Visual =~ x1 0.762 0.120 0.571 0.965 1.002 1106
## Visual =~ x2 0.559 0.105 0.395 0.731 1.001 2093
## Visual =~ x3 0.756 0.117 0.572 0.957 1.001 1166
## Visual =~ x4 0.023 0.071 -0.083 0.151 1.001 1704
## Visual =~ x5 -0.061 0.086 -0.217 0.051 1.002 1698
## Visual =~ x6 0.055 0.073 -0.043 0.190 1.001 1661
## Visual =~ x7 -0.140 0.149 -0.427 0.032 1.001 1174
## Visual =~ x8 0.041 0.115 -0.131 0.251 1.003 1245
## Visual =~ x9 0.314 0.124 0.095 0.509 1.002 1290
## Verbal =~ x1 0.136 0.110 -0.016 0.330 1.002 1028
## Verbal =~ x2 0.013 0.068 -0.093 0.130 1.001 1861
## Verbal =~ x3 -0.078 0.098 -0.267 0.045 1.001 1268
## Verbal =~ x4 0.987 0.076 0.866 1.112 1.003 2036
## Verbal =~ x5 1.137 0.085 1.007 1.286 1.003 1675
## Verbal =~ x6 0.896 0.074 0.774 1.019 1.001 1427
## Verbal =~ x7 0.025 0.073 -0.079 0.152 1.001 2025
## Verbal =~ x8 -0.028 0.069 -0.150 0.069 1.000 1921
## Verbal =~ x9 0.013 0.060 -0.081 0.114 1.003 2150
## Speed =~ x1 0.036 0.083 -0.076 0.190 1.002 1757
## Speed =~ x2 -0.051 0.079 -0.198 0.055 1.002 2051
## Speed =~ x3 0.030 0.077 -0.077 0.167 1.002 2124
## Speed =~ x4 0.004 0.057 -0.089 0.101 1.001 2195
## Speed =~ x5 0.004 0.065 -0.097 0.108 1.001 1826
## Speed =~ x6 0.002 0.054 -0.087 0.092 1.001 2033
## Speed =~ x7 0.760 0.120 0.579 0.966 1.001 1186
## Speed =~ x8 0.762 0.104 0.593 0.941 1.000 1498
## Speed =~ x9 0.507 0.095 0.355 0.672 1.003 1558
## ───────────────────────────────────────────────────────────────────────────────
## Inter-factor correlations
## ───────────────────────────────────────────────────────────────────────────────
## Verbal ~~ Visual 0.362 0.123 0.151 0.552 1.003 1126
## Speed ~~ Visual 0.284 0.168 -0.010 0.550 1.003 1251
## Speed ~~ Verbal 0.224 0.118 0.033 0.409 1.001 1563
## ───────────────────────────────────────────────────────────────────────────────
## Residual variances
## ───────────────────────────────────────────────────────────────────────────────
## x1 ~~ x1 0.668 0.128 0.452 0.860 1.002 1217
## x2 ~~ x2 1.090 0.115 0.901 1.281 1.000 2791
## x3 ~~ x3 0.737 0.133 0.514 0.945 1.000 1326
## x4 ~~ x4 0.375 0.086 0.228 0.509 1.004 1373
## x5 ~~ x5 0.431 0.110 0.248 0.609 1.004 1459
## x6 ~~ x6 0.370 0.076 0.253 0.492 1.002 1090
## x7 ~~ x7 0.660 0.134 0.434 0.870 1.002 1110
## x8 ~~ x8 0.457 0.125 0.237 0.640 1.001 1308
## x9 ~~ x9 0.570 0.075 0.450 0.692 1.000 2046
## ───────────────────────────────────────────────────────────────────────────────
##
##
## Column names: from, op, to, mean, sd, 5%, 95%, rhat, ess_bulkThe effect of minor factors is small, RMSE = 0.024. The original hypothesized loadings maintain their relation to their hypothesized factors. Of the cross-loadings, only the relation from the visual factor to x9 is non-trivial, with most being very close to 0. Additionally, the interfactor correlations have all reduced from the original basic CFA, suggesting that forcing cross-loadings to zero artificially inflated interfactor correlations (Ferrando and Lorenzo-Seva 2000).